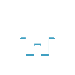这题相当于是这五个相邻的省份,用四种颜色标注,而且相邻的两个省份不能使用同一种颜色,问一共有多少种着色方法。
这一道题考的是排列组合,而用这种方式来考排列组合,在高考了还是第一次,所以也被认为是一道“神题”!
然而对于考生而言,神题就是用来问候命题人全家的!
考生在经历过前面超纲的题目,复杂的运算,选择题三联爆,再遇到这种神题,心态要是还能稳得住,真的要敬你是条憨子!
眼镜考生便是如此,此时他的心态,已经处于崩溃的边缘。
终于熬到过了填空题,来到后面的大题,此时考试时间已经用掉了大半。
眼镜考生看了看墙上的挂钟,他已经意识到,时间不够用了,剩下的时间,很难完成全部的题目。
眼镜考生望向了第一道大题:“已知复数Z的辐角为60度,且|z-1|是|z|和|z-2|的等比中项,求|z|。”
有点懵,先放一放。
“某海滨城市附近海绵有一台风,当前台风中心位于城市O(如图)的东偏南θ(θ=arccos根号2/10)方向300KM的海面P处……”
著名的台风题,一看就不会做。
“已知常数a大于0,在矩形ABCD中,AB=4,BC=4a,O为AB的中点,点EFG分别在BC、CD、DA上……”
高考数学难度天花板,史上最难高考的最难一题,经典“神题”!
“神题”出现意味着,命题人好欠抽!
一种绝望的感觉,从眼镜考生心头升起,此时的他已然是袁华附体,这道题,我不会做!
……
2003年高考的数学,是有史以来高考难度最大的数学考试。原因就是因为在2003年高考前夕,发生了一次试题泄密事件。
我们国家的机密等级分为绝密、机密和秘密三个级别,而高考试卷恰好是最高的绝密级别,跟核武器的资料是同级的。
即便是开考以后,只要没有到收卷时间,高考试卷依旧是机密级别,是不允许泄露的。
所以在高考的时候,即便是考生提前交卷,也不允许离开考点,考试结束前泄题的,都算是泄密。
理论上这么高的保密级别,是不可能出现高考试卷被盗窃的情况。然而在2003年,高考前两天,却发生了高考试卷被盗的案件。
于是教育部决定启用备用试卷。640万考生的命运,就此被改变。
结果就是理科的数学备用试题,难度堪比奥数级别。普通学生哪里做过这种难度的题目,见到试卷直接就懵圈了!
即便是会做题,但考试的时间也不够用,题目根本做不完,后面几道数学题空着一大半。
无数的考生考完数学,直接心态爆炸。
那一年考生的数学平均分数不到六十分,如果你能考及格,已经是一流的数学成绩了。
而且2003年高考的数学全国卷,没有满分。
其他年份的高考数学,虽然也有很难的,但多少都会有些优秀考生拿到满分。
考生中可不缺乏训练过奥数的同学,这些奥数生的数学水平,比普通考生高了好几个档次,而全国那么多奥数生,却没有一个能拿到满分。
这也从侧面说明了,2003高考数学,绝对是当之无愧的最强难度!